Vai all’indice

Dopo la breve introduzione fatta la volta scorsa, cominciamo il nostro “viaggio” attraverso  i segreti della scorrevolezza degli pneumatici.

Ammettiamolo, tra tutti gli argomenti che riguardano la nostra mountain bike, questo è quello che più di tutti ci lascia sistematicamente in balìa di leggende metropolitane e spiegazioni al confine tra la stregoneria e l’esoterico. A giustificazione di coloro che, convinti di elargirci preziose perle di scienza, ci rifilano sgangherati sproloqui che violano i principi della dinamica ma anche del buon senso, c’è il fatto che la materia è davvero complicata. Io stesso, che pure mi occupo di queste materie per lavoro, e fortunatamente mi diverto a scandagliare tra i meandri della meccanica applicata alla mountain bike, ho sempre rimandato di affrontare lo studio della quantificazione dell’attrito volvente, ovvero del determinare quanto diavolo vale questa azione resistente al variare di tipologia di terreno, formato dei copertoni, pressioni di gonfiaggio e tante altre variabili che entrano in gioco in questa materia. Sapevo che rappresentare tutto ciò attraverso dei modelli matematici (che altro non sono che una miriade di formule che descrivono i fenomeni fisici che si  verificano quando una ruota… rotola!) sarebbe stato un lavoraccio (bello, ma comunque un lavoraccio). E infatti così è stato!

A farmi decidere ad analizzare finalmente il fenomeno è stato un episodio avvenuto quest’estate, quando durante una notturna ho notato che alcune amiche avevano gli pneumatici talmente sgonfi che sembrava pedalassero su delle spugne.  Mi avevano spiegato che la guida del gruppo con cui escono abitualmente, aveva dato loro l’indicazione di adottare quel valore di pressione. Ci sono situazioni, come quando si pedala sulla ghiaia di una massicciata ferroviaria,  in cui valori di pressione decisamente bassi consentono di faticare meno. Fatto salvo per situazioni simili, su strade e sentieri “normalmente sconnessi”, valori di pressione come quelli utilizzati da quelle amiche servono solo a sfiancarsi inutilmente.

Ma di tutte queste cose parleremo abbondantemente più avanti, quindi per il momento vediamo di introdurre l’argomento spiegando cosa è questo benedetto attrito volvente, colpevole di una buona parte della nostra fatica in sella.

Vi suggerisco innanzitutto di dare uno sguardo a questa pagina del sito della Schwalbe, sia perché ci sono alcuni cenni generali su cosa è l’attrito volvente, sia perché nel corso dei nostri articoli ci divertiremo a contraddire alcune affermazioni fatte dalla stessa Schwalbe. In particolare, vedremo come l’affermazione che “pneumatici più larghi abbiano una minore resistenza al rotolamento” sia una verità parziale, ovvero ne nasconda una parte, e questo significa mistificare la realtà. Brutalizzando: è uno slogan commerciale travestito da “verità” scientifica.

Per aiutarvi a comprendere che cosa sia l’attrito volvente, voglio descrivervelo in una maniera estremamente semplice:

innanzitutto, considerate che lo pneumatico, grazie all’aria al suo interno, è un materiale elastico. Questo significa che è in grado di variare la propria geometria, comprimendosi ed espandendosi. A causa del peso che grava su di esso (che di norma è quello della bici più quello del ciclista, suddiviso sulle due ruote), lo pneumatico si “schiaccia” nella parte a contatto col terreno. Accade così che, quando il biker sale sul suo bolide, gli pneumatici subiscono questo schiacciamento nel punto di contatto ruota/suolo. Allo stesso modo, quando il biker scende dalla bici, lo pneumatico espande nuovamente la propria geometria sollevandosi. Riceve quindi una spinta diretta verso l’alto.

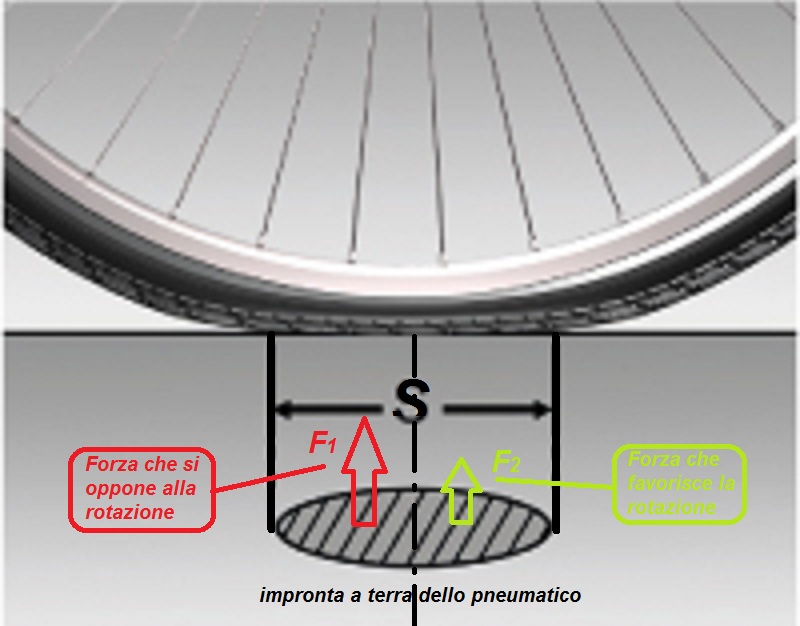
Bene, a questo punto siamo pronti per comprendere cosa accade quando la ruota… ruota. In questo caso, dobbiamo pensare allo pneumatico come se fosse composto da un insieme di molle disposte lungo la sua circonferenza. Supponiamo allora che, durante la rotazione, ci siano sempre due di queste molle a contatto col suolo. Provate a immaginare cosa accade a queste due molle quando lo pneumatico ruota: la molla che si trova davanti viene schiacciata dalla rotazione della ruota mentre, sempre grazie alla rotazione, la molla che sta dietro si allunga. Abbiamo quindi che la molla posta anteriormente esercita una forza che si oppone alla rotazione, mentre la molla posteriore spinge favorendo la rotazione.

Se queste due forze, opposte, fossero di pari valore, si annullerebbero reciprocamente e la ruota non verrebbe in alcun modo influenzata nel suo moto (l’opposizione al moto della molla anteriore verrebbe perfettamente equilibrata dalla spinta della molla posteriore).

Ecco, l’attrito volvente nasce proprio dal fatto che queste due forze, ahinoi, non sono di pari valore. Infatti, la molla posteriore, estendendosi, non riesce a “restituire” la forza che in precedenza aveva “subito” quando, trovandosi anteriormente, era stata compressa. Questa differenza tra le due forze, che si manifesta in una forza risultante che si oppone alla rotazione, è proprio il nostro attrito volvente.

Adesso lasciate perdere la ruota rivestita di molle che ci è tornata utile per la nostra schematizzazione, e pensate allo pneumatico.

Considerate la parte dello pneumatico, schiacciata, che si trova a contatto col suolo. Considerate questa superficie, che si chiama superficie di appoggio, divisa in due metà: quella anteriore corrisponderà alla molla che viene schiacciata durante il rotolamento, e quella posteriore alla molla che si estende. La parte posteriore non è in grado di restituire tutta l’energia che aveva ricevuto quando era stata compressa; ne restituisce solo una parte, perché la restante viene “sprecata” da fenomeni fisici che avvengono al suo interno e che la trasformano in calore. Ecco quindi, ancora una volta, che solo una parte dell’energia usata per comprimere lo pneumatico viene restituita quando questo si espande. Quella restante, andata perduta, va compensata (ovvero fornita) dalle nostre povere gambe. Questo è l’attrito volvente.

A questo punto, dato che la descrizione fisica dell’attrito volvente è un argomento che si affronta in un qualunque corso di fisica delle scuole superiori (e quindi dovremmo averlo studiato tutti), chi ha voglia di rinfrescarsi la memoria troverà materiale in abbondanza disponibile in rete.

Noi invece adesso andiamo oltre, e vediamo di analizzare quali sono le conseguenze dell’attrito volvente nel comportamento dinamico della bicicletta.

Come prima cosa, sottolineiamo un aspetto fondamentale che analizzeremo nelle prossime puntate: il valore del coefficiente d’attrito dipende dalla pressione dello penumatico, dalla tassellatura e dalle condizioni del fondo stradale. Questo significa che le ruote della nostra mountain bike vanno messe a punto in modo differente a seconda del tipo di terreno in cui si deve pedalare.

Questa premessa è fondamentale per sottolinearvi che questo argomento non deve essere affrontato in termini “assoluti” (ovvero, pensare erroneamente che esista un “settaggio” universalmente giusto, in grado di ottimizzare il funzionamento dinamico della mtb in tutte le situazioni), ma deve invece essere affrontato in termini relativi (e quindi devo innanzitutto pensare a dove voglio pedalare con la mia mtb, e la messa a punto va fatta relativamente a quelle specifiche condizioni che troverò in quel determinato contesto).

In questa prima puntata cominceremo quindi col descrivere come si determina il coefficiente d’attrito volvente quando si pedala su un fondo stradale regolare, ovvero su asfalto o su sterrato perfettamente battuto. I risultati che otterremo saranno alla base delle analisi che affronteremo successivamente, quando andremo a vedere come si determina l’attrito volvente al variare delle “condizioni di dissesto” del suolo su cui si pedala. In quella fase, vedremo quindi come vanno scelti i valori di pressione e il tipo di tassellatura ottimali per ciascuna specifica situazione.

Per cominciare la nostra analisi, consideriamo innanzitutto ruote equipaggiate con copertoni lisci o con battistrada di tipo stradale (ovvero non tassellato, ma con scanalature volte a migliorare l’aderenza su bagnato o su sterrati con fondo stradale regolare).

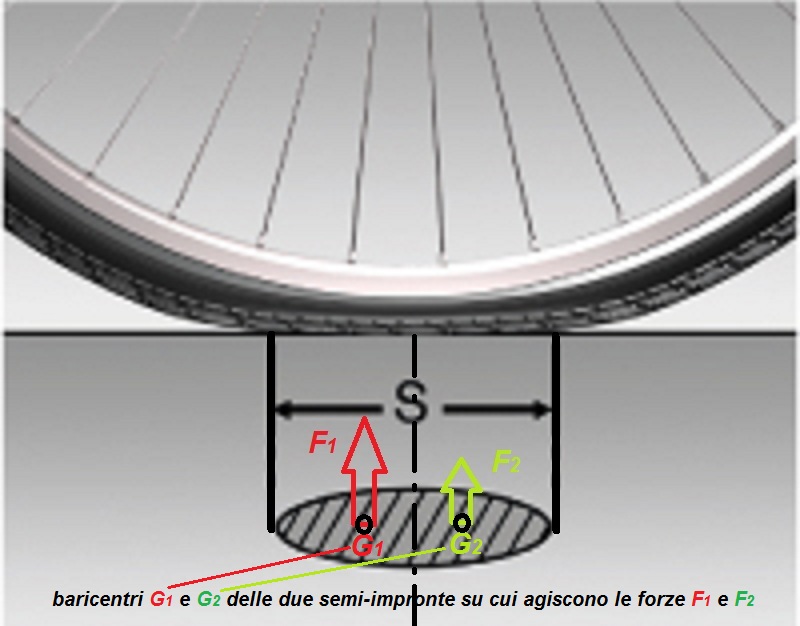
Come si vede dall’immagine, le due forze che agiscono sulla superficie di contatto ruota/suolo sono applicate nei baricentri delle due semi-impronte perfettamente simmetriche. La dimensione dell’impronta è funzione della pressione dello pneumatico e del peso che grava su ciascuna ruota. Ricordiamoci infatti che la pressione (che indichiamo con “p”) è una forza per unità di superficie. Allora, quando la ruota è sottoposta a un peso “P”, lo pneumatico si “schiaccia” fino a che l’impronta assume un valore della propria superficie pari a “S”, tale che la forza ottenuta moltiplicando  p*S (che è la spinta che lo pneumatico esercita verso l’alto) sia uguale al peso che grava sulla ruota (che è una forza diretta verso il basso, e che in questo modo viene equilibrata).

Bene, poiché quindi Peso=pressione*Superficie, e considerando il peso costante (è il peso di bici+biker distribuito sulle due ruote), è chiaro che, se diminuisce la pressione dello pneumatico, dovrà aumentare la superficie dell’impronta per far si che il prodotto p*S resti costante. In pratica,  pressione e Superficie sono inversamente proporzionali (banalizzando, significa che se la pressione dimezza, la superficie raddoppia).

Puntiamo adesso la nostra attenzione sui due baricentri G1 e G2 delle semi-impronte.  Nel baricentro G1 agirà la forza F1 che si oppone al moto, mentre su G2 agirà la forza F2 che lo favorisce. Al variare della distanza dei due baricentri dal centro dell’impronta, aumenterà il momento delle due forze agenti su di essi. Se aumenterà questo momento, che equivale alla resistenza al rotolamento che agisce sulla ruota, aumenterà conseguentemente l’attrito volvente.

Il nostro obiettivo è quindi quello di determinare il legame tra la variazione del momento resistente e la variazione della pressione di gonfiaggio. Il problema si risolve in modo abbastanza semplice, ovvero: la superficie dell’impronta varia in modo inversamente proporzionale al valore della pressione di gonfiaggio; la distanza baricentrica varia proporzionalmente alla radice quadrata della superficie dell’impronta (vi risparmio la dimostrazione geometrica, anche se è piuttosto semplice e, chi vorrà, potrà ricavarsela come facile esercizio).

Da queste due premesse, si ottiene quanto da noi cercato, ovvero: il coefficiente d’attrito volvente (direttamente legato alla distanza baricentrica) varia in modo inversamente proporzionale alla radice quadrata della variazione di pressione.

Passiamo subito ad analizzare un caso concreto, così che possiate rendervi conto dell’estrema semplicità di questa formula, che ciascuno di voi potrà applicare con grande facilità.

Consideriamo un copertone con battistrada scanalato da 1.75 come il Michelin Country Rock della foto, ovvero il classico pneumatico per bici da trekking o per mountain bike con allestimento “soft” da pista ciclabile. Per uno pneumatico come questo, considerando un biker di circa 70-75kg di peso, il valore di pressione massima da utilizzare è di 4,5bar (valori superiori migliorerebbero la scorrevolezza su asfalto, ma la peggiorerebbero sulle pur minime irregolarità di una ciclabile sterrata anche con un fondo perfetto; su questo argomento torneremo nelle prossime puntate). Il valore del coefficiente d‘attrito volvente determinato in laboratorio per queste condizioni, e che noi utilizzeremo come riferimento, è cff.a.v.=0,007, valido quando si pedala su asfalto. Supponiamo di voler portare la pressione da 4,5bar a 3bar (il motivo potrebbe essere che si deve usare la bici su un terreno più irregolare, dove una pressione di 4,5bar incrementerebbe la resistenza al moto; anche queste cose le analizzeremo nel dettaglio nelle prossime puntate), in questo caso il rapporto tra le pressioni iniziale e finale sarebbe pari a 4,5/3=1,5. Il coefficiente d’attrito volvente allora avrebbe un incremento pari alla radice quadrata di 1,5, che è pari a 1,22 (il che equivale a dire che si ha un incremento del 22%), e si avrebbe quindi cff.a.v.=0,7*1,22=0,854

Come detto, in questo caso si è deciso di abbassare la pressione per migliorare la scorrevolezza su terreno sconnesso, ottimizzando la situazione (e anche questo, nelle prossime puntate, vedremo come va fatto). Chiaramente, la minor pressione comporta una penalizzazione nei tratti del nostro itinerario in cui si pedala su asfalto. Supponendo di pedalare a 30km/h, poiché a questa velocità l’attrito volvente incide per circa il 30% sulla potenza complessiva che il nostro “motore” deve erogare, avremo che l’incremento di potenza dovuto all’attrito volvente sarà, percentualmente, pari a 0,22*30%=6,6% (o, se preferite, a parità di potenza erogata si viaggerà a 29,5km/h invece che a 30km/h).

Bene, direi che per il momento possiamo fermarci qui. Quanto visto vi ha consentito di prendere confidenza con l’argomento. Nella prossima puntata proseguiremo la nostra analisi, a partire dalla determinazione dei valori di pressione da utilizzare, differenti a seconda del peso di biker+bici (altro motivo per cui le generiche indicazioni del tipo “sulle bdc la pressione va a 8.5bar,” o “la pressione ideale per le gomme da mtb è 1.8bar” non hanno alcun senso); la nostra analisi ci porterà via via a scoprire come determinare il coefficiente d’attrito per tutte le tipologie di pneumatici, da quelli delle bici da corsa alle coperture tassellate delle mountain bike. Vedrete che, un passo alla volta, sarete in grado di scegliere al meglio i copertoni per la vostra bici e la relativa pressione di gonfiaggio, effettuando una messa a punto ottimale in base alle tipologie di fondo stradale che dovrete affrontare in ciascuna escursione.

State sintonizzati, ci risentiremo prestissimo

Stefano Tuveri

PROSEGUE CON LA SECONDA PUNTATA: COME DETERMINARE LA PRESSIONE “GIUSTA” PER LE BICI DA CORSA