SEGUE DALLA PRIMA PUNTATA SU: COME DETERMINIAMO IL COEFFICIENTE D’ATTRITO VOLVENTE
La volta scorsa abbiamo visto cosa è l’attrito volvente, e soprattutto qual è la sua origine dal punto di vista meccanico.
In questa nuova puntata ci occuperemo invece di determinare i giusti valori di pressione per le coperture lisce o con battistrada non tassellato. In pratica, ci occuperemo delle coperture per le bici da corsa e, successivamente, degli pneumatici per quelle tipologie di bici utilizzate prevalentemente su asfalto e piste ciclabili (sia sterrate che asfaltate), quali le trekking bike o le stesse mountain bike in allestimento “leggero”.
Le coperture tassellate saranno invece esaminate più avanti, dato che l’argomento è decisamente più complesso a causa della grande varietà di tipologie di fondo stradale su cui vanno utilizzate, nonché delle tante tipologie di tassellature e dimensioni dei copertoni in commercio (è sufficiente consultare il catalogo di un qualunque produttore per rendersi conto della grande scelta oggi disponibile). La messa a punto dei copertoni “lisci”, oltre che utile per tutti coloro che li utilizzano, sarà quindi propedeutica per occuparci successivamente di quelli tassellati.
Cominciamo quindi col determinare la pressione corretta da utilizzare per le coperture delle biciclette da corsa. Consideriamo la tipologia di tubolare più sottile, che è quella da 18mm, oggi praticamente non più utilizzato ma che ci torna utile per i nostri calcoli. In questo modo, partendo dalla situazione limite (appunto 18mm), vediamo come si rilevano i valori di pressione corretti per qualunque altro spessore.
Partiamo dal dato sperimentale rilevato per il coefficiente d’attrito volvente: si rileva che, in un tubolare da 18mm su cui grava un peso di 42,5kg (ovvero un peso di bici+ciclista pari a 85kg, diviso sulle due ruote), la pressione degli pneumatici ottimale (poi vedremo cosa si intende per “ottimale”) è pari a 8,5bar.
In questo modo si ha un valore del coefficiente pari a 0,0034, che è il coefficiente d’attrito volvente più basso che è possibile ottenere per l’utilizzo su strada di una bdc (su pista, invece, il coefficiente è decisamente più basso, pari a 0,0021). Questo valore del coefficiente d’attrito è quello che, in parole povere, assicura la miglior scorrevolezza alla bici, ovvero consente di fare la minor fatica possibile (o, se preferite, a parità di fatica consente la maggior velocità possibile).
La domanda a questo punto è: dato che ciascun ciclista ha il suo peso, e altrettanto vale per le bici (e quindi non posso applicare pedissequamente un valore standard di pressione, che chiaramente non può andare bene per tutti) quale pressione devono avere gli pneumatici al variare del peso che grava sulle ruote, per poter continuare ad avere la miglior scorrevolezza possibile (ovvero il coefficiente d’attrito volvente minimo, pari come detto a 0,0034)?

Va innanzitutto detto che, variando il peso, noi dobbiamo variare anche la pressione in modo che, su quello stesso tubolare da 18mm, la superficie dell’impronta a terra resti costante (anche in questo caso, il motivo lo vedremo più avanti). Ricordiamoci quanto avevamo mostrato la volta precedente, ovvero che il peso che grava sulla ruota è equilibrato dal valore del prodotto di (pressione)*(Superficie impronta), ovvero: P=p*S. Da questa formula si vede come, dato che “S” deve restare costante, allora il peso “P” e la pressione “p” devono variare proporzionalmente affinchè l’equazione resti valida.
Questo significa, molto semplicemente, che se il peso aumenta ad esempio del 20%, anche la pressione dovrà aumentare della stessa percentuale del 20%.
Vediamo un esempio pratico: innanzitutto armiamoci di una bilancia pesa-persone e, saliti in sella alla bici, saliamo sulla bilancia prima con una ruota e poi con l’altra. I due pesi che leggiamo sono quelli che gravano su ciascuna delle due ruote.
Per fare la pesata, assumete in sella la posizione che di norma tenete quando pedalate. Innanzitutto noterete che il peso che grava sull’anteriore è più basso rispetto a quello sulla posteriore. Di norma, sull’anteriore graverà il 40-45% del peso totale, sulla posteriore il 55-60%.
Supponiamo di avere un ciclista leggero, di circa 60kg, e quindi un’accoppiata bici+ciclista da 70kg. E’ verosimile avere sulla ruota anteriore un peso di 32kg e sulla posteriore di 38kg.
Possiamo a questo punto determinare i corretti valori di pressione sulle due ruote: per l’anteriore, il rapporto tra i 32kg rilevati e i 42,5kg che sono il nostro riferimento è pari a 32kg/42,5kg=0,75. Allora anche la pressione di riferimento, pari a 8,5bar, va moltiplicata per 0,75, Si ottiene che, per la situazione presa in esame, la pressione all’anteriore deve essere pari a 6,4bar.
Ragionando allo stesso modo sulla posteriore, si ha: 38kg/42,5kg=0,89. Moltiplicando 8,5bar per 0,89, si ottiene per la posteriore un valore della pressione pari a 7,6bar.
La domanda successiva è: se varia la larghezza dello pneumatico, come si determina la corretta pressione? In questo caso, bisogna tener conto che, per trovarci sempre nelle condizioni ottimali, deve rimanere uguale la lunghezza dell’impronta al suolo. Il motivo lo vedremo più avanti, per il momento ci basti sapere che quindi, a copertone più largo, corrisponderà un’impronta che si allarga a sua volta. Evito di descrivervi la trattazione geometrica con cui si determina di quanto l’impronta si allarghi. Mi limito a darvi il risultato finale, ovvero: a parità di lunghezza dell’impronta, la sua larghezza è proporzionale alla radice quadrata della larghezza dello pneumatico. Vediamo di seguito un caso pratico, perché la cosa è più semplice a farsi che a dirsi.
Prima però, a proposito di quanto appena visto, va fatta una considerazione: la Schwalbe, nel proprio sito internet, afferma che uno pneumatico più largo consente un minor coefficiente d’attrito. Trovate la loro motivazione in questa pagina. In realtà, più avanti vedremo come, sotto il profilo scientifico, quest’affermazione è errata, peraltro anche in modo grossolano, perché ignora quella che è l’origine meccanica e dinamica dell’attrito, appoggiandosi a una descrizione “scolastica” che va bene solo per introdurre il concetto di attrito volvente agli studenti delle scuole superiori (mentre invece, ahinoi, l’attrito è una gran rottura di scatole ben più complessa). Ma per il momento vi lascio con questo dubbio in sospeso, che vi chiarirò la prossima volta con una spiegazione intuitiva che coglierete facilmente, mentre adesso vediamo di sistemare la pressione della nostra bdc.
Passiamo allora a un caso pratico: supponiamo che il ciclista visto prima (quello da bici+ciclista=70kg) utilizzi pneumatici da 23mm; il rapporto rispetto a quelli da 18mm considerati prima è pari a 23/18=1,28; allora la pressione rilevata prima va divisa per la radice quadrata di 1,28, che è pari a 1,13. Dividerò quindi i valori di pressione rilevati prima (per i tubolari da 18mm) per 1,13 e avrò: all’anteriore, 6,4bar/1,13=5,7 bar; alla posteriore, 7,6bar/1,13=6,7bar.
Bene, dato che a questo punto vi si saranno già incrociati gli occhi dietro a tutti questi numeri, vediamo di riassumere il tutto nello schema qui sotto, e vedrete che il procedimento è estremamente semplice.
Procedete come segue:
- innanzitutto salite in sella alla bici e mettete una classica bilancia pesa-persone prima sotto una ruota e poi sotto l’altra, in modo da rilevare il peso che deve sopportare ciascuna di esse. Supponiamo che rileviate 36kg all’anteriore e 44kg alla posteriore
- dividete il peso rilevato su ciascuna ruota, per il peso di riferimento di 42,5kg. Nel nostro caso otterremo i seguenti coefficienti: 36kg/42,5kg=0,85 all’anteriore e 44kg/42,5kg=1,04 alla posteriore
- moltiplicate la pressione di riferimento, pari a 8,5bar, per i due coefficienti trovati sopra: all’anteriore risulterà una pressione di 8,5*0,85=7,2bar; alla posteriore una pressione di 8,5*1,04=8,8bar
- i valori di pressione trovati, sono quelli giusti per un tubolare da 18mm. Se noi utilizziamo uno pneumatico di larghezza differente, dobbiamo determinare il coefficiente correttivo dividendo la larghezza di riferimento di 18mm per la larghezza del nostro pneumatico, e calcolando la radice quadrata. Allora, supponendo di usare gomme da 23mm, il rapporto sarà pari a 18/23=0,78. Il coefficiente moltiplicativo si ottiene estraendo la radice quadrata di 0,78, che è =0,88
- per trovare le pressioni corrette per i nostri pneumatici da 23mm, moltiplichiamo le pressioni rilevate precedentemente per il coefficiente 0,88. Per l’anteriore troviamo che la pressione corretta è 7,2*0,88=6,3bar, per la posteriore otteniamo 8,8*0,88=7,7bar
Se date uno sguardo a questa pagina del sito della Continental, potete notare come i valori che abbiamo determinato scientificamente, cadono nell’intervallo di valori di pressione consigliati dalla Continental per le sue coperture (occhio che i valori sono espressi in psi; per convertirli in bar dovete dividerli per 1,4). Il vantaggio, seguendo il criterio scientifico che vi ho descritto, è che potete determinare la pressione corretta con precisione, invece di dover scegliere “a occhio” un valore che cada nell’intervallo proposto dai produttori di pneumatici.
Vi avevo promesso che vi avrei spiegato da dove nascono le formule che vi ho proposto. In particolare, voglio spiegarvi perchè non si debba superare il valore di pressione che abbiamo determinato con la nostra procedura. Quel valore, infatti, è da considerarsi come quello della pressione limite oltre la quale il coefficiente d’attrito volvente aumenta, con un paradosso in realtà solo apparente in quanto ha una ben precisa ragione scientifica (tranquilli, vi spiegherò il tutto in modo intuitivo, non vi farò sostenere un esame di Costruzioni di Macchine).
In pratica, una volta, determinato il valore “giusto” della pressione, la scorrevolezza della ruota peggiore per pressioni più basse (perché aumenta la superficie dell’impronta e, come visto nella precedente puntata, questo aumenta il momento resistente e, di conseguenza, l’attrito volvente). Peggiora però anche per pressioni più alte, e questo potrebbe apparire un controsenso.
Vediamo allora di spiegare che cosa determina questa pressione limite.
Innanzitutto, va detto che nella descrizione dell’attrito in una trattazione “scolastica”, si considera la superficie di contatto come perfettamente piatta. Questa è tuttavia un’astrazione teorica, dato che una superficie come quella stradale del nostro caso, tutto è fuorchè liscia. E’ invece costituita da “irregolarità regolarmente distribuite”, come chiunque di noi può rilevare osservando l’asfalto.
Questo significa che lo pneumatico poggia su un certo numero di sporgenze che emergono rispetto al piano medio dell’asfalto.
La trattazione fisico-matematica di come venga determinato l’attrito volvente a causa dell’interazione pneumatico/irregolarità è piuttosto complessa e richiede conoscenze specifiche che si acquisiscono solo con un percorso di studi universitario e post-universitario, per cui esula dagli obiettivi di questo articolo. Quello che farò di seguito è pertanto tradurvi con argomentazioni intuitive il risultato degli studi che ho effettuato sull’argomento.

Nell’immagine, vi rappresento schematicamente quella che è la situazione di rotolamento ideale per uno pneumatico. Come vedete, la pressione dev‘essere tale da consentire alla copertura di deformarsi in corrispondenza dell’irregolarità del terreno “1”, posta in posizione centrale. Questa deformazione, consentirà un abbassamento della ruota (parliamo di un abbassamento minimo, dell’ordine del decimo di millimetro) che permette allo pneumatico di andare a contatto anche con le due irregolarità laterali, indicate con “2” e “3”. In questo modo, durante il rotolamento, la ruota può fruire di un passaggio graduale da un punto di contatto a quello adiacente (nel caso la nostra ruota vada verso sinistra, avremo che il peso gravante sulla ruota si trasferirà in modo graduale dal punto di contatto con l’irregolarità “1” a quello con l’irregolarità “2”).
Mi raccomando, ricordiamoci che quella dell’immagine è una schematizzazione in cui le irregolarità sono volutamente accentuate per comprendere meglio cosa concettualmente attuale. Nella situazione reale, lo pneumatico grazie alla deformazione sarà in grado di “avvolgere” le irregolarità dell’asfalto, “spalmandovisi” sopra e consentendo che la superficie di appoggio assuma la forma simil-ellittica già vista (e riportando quindi il tutto alla situazione vista nella prima puntata, con le due forze che agiscono sui baricentri delle semi-superfici, generando la resistenza al rotolamento)
Intuitivamente, comprendete che questa continuità nel trasferimento del peso tra ruota e terreno crea un rotolamento regolare. Analizzando questo fenomeno meccanico sotto il profilo fisico-matematico, si ricava che quella condizione di rotolamento è quella che corrisponde alla resistenza di rotolamento più bassa possibile. Qualunque scostamento da questa condizione, dovuta sia a una pressione più bassa che a una pressione più bassa, ci allontana da queste condizioni ottimali, aumentando la resistenza al rotolamento (ovvero, aumentano il coefficiente d’attrito volvente).

Per farvi comprendere ancora meglio cosa accade, nell’immagine qui sopra consideriamo cosa avviene quando si aumenta la pressione oltre il valore limite. A causa della maggiore pressione, lo pneumatico non si deformerà a sufficienza per consentire, quando poggia sull’irregolarità centrale “1”, di andare a contatto anche con le irregolarità laterali “2” e “3”. In questo modo, nel rotolamento, il passaggio da un punto di contatto all’altro non avviene più con continuità (come invece nel caso, ideale, visto in precedenza). Si ha invece un passaggio da un punto di contatto all’altro fatto di “attacchi e stacchi” (supponendo di andare verso sinistra, la ruota sta sospesa su “1”, fino a che non poggia su “2”, e a quel punto abbandona bruscamente il punto di contatto “1” stando sospesa su “2”, per poi raggiungere il successivo punto adiacente). L’effetto, giusto per usare un’immagine che vi aiuti a comprendere intuitivamente quanto accade, è quello di una ruota “squadrata”, ovvero come se non fosse circolare ma posse un poligono composto da tanti piccoli lati (lunghi quanto la distanza tra le irregolarità dell’asfalto). Sapete per esperienza che far rotolare un poligono è senza dubbio più faticoso che far rotolare una circonferenza. Bene, si dimostra che aumentando la pressione oltre il valore limite, la resistenza al rotolamento aumenta gradualmente fino ad arrivare al 50% in più.
Per chiudere, come vi avevo promesso voglio mostrarvi perché l’affermazione della Schwalbe (ovvero che ruote più larghe determinano una minore resistenza al rotolamento) è un buon spot commerciale, ma è scientificamente errata (diciamo pure che è una sciocchezza).
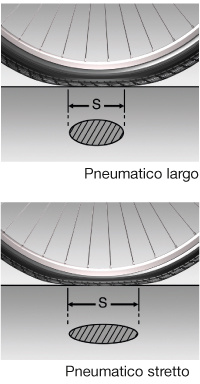
La spiegazione è proprio in ciò che abbiamo visto qua sopra: una impronta al suolo più corta determina un minor coefficiente d’attrito se ci si attiene alla trattazione scolastica che, come visto, è un’astrazione teorica (laddove la realtà è ben diversa e più complessa). Intuitivamente, vi rendete conto che una impronta al suolo più lunga consente di raggiungere le irregolarità adiacenti a quella del punto d’appoggio centrale (ovvero, nella nostra schematizzazione, la “2” e la “3” della nostra figura), permettendo un moto di rotolamento uniforme (quello che, come visto, consente la miglior scorrevolezza possibile). Uno pneumatico più largo, a parità di pressione, ha un’impronta al suolo più corta, e allora per far si che l’impronta possa raggiungere le irregolarità “2” e “3” si deve abbassare la pressione (e in questo modo, ancora una volta, lo pneumatico riesce a “spalmarsi” sull’asfalto, generando la superficie d’appoggio simil-ellittica, ovvero la geometria che corrisponde alle condizioni di rotolamento ideali descritte nella prima puntata). La pressione “giusta”, che consente il rotolamento uniforme, è quella che abbiamo imparato a determinare nella procedura descritta più sopra. Accennando invece alla trattazione fisico-matematica, si rileva (ma chiaramente non vi infliggo la dimostrazione) come uno pneumatico più largo, a parità di pressione, consenta una deformazione minore sul punto d’appoggio centrale “1”. In questo modo, perché lo pneumatico riesca ad andare a contatto anche coi punti “2” e “3”, si deve abbassare la pressione (e il valore di pressione “giusto”, ovvero che consente quest’abbassamento, è proprio quello che si calcola con la procedura vista più sopra).
Un’ultima cosa che voglio sottoporre alla vostra attenzione è questa: la superficie di contatto ruota/asfalto è davvero piccolissima. La sua forma è assimilabile a un’ellisse, con asse maggiore (ovvero la lunghezza dell’impronta) di 62,8mm (in pratica poco più di un centimetro) e asse minore (ovvero larghezza dell’impronta) che, per tubolari da 18mm, è pari a 10,2mm, e per larghezze maggiori è via via crescente. Stiamo quindi parlando di una superficie d’appoggio piccolissima, per cui vi rendete benissimo conto da soli di quanto risenta dell’influenza delle seppur piccole irregolarità dell’asfalto (anche quando questo è in ottime condizioni).
Bene, direi che questa puntata, dedicata agli stradisti, possiamo chiuderla qui. Adesso avete un criterio che vi consente di determinare la pressione “giusta” rilevata su misura per quelle che sono le vostre caratteristiche (ovvero il peso vostro e della vostra bici, più eventuali bagagli al seguito).
La prossima volta ci occuperemo delle ruote più larghe, partendo da quelle non tassellate ma con battistrada, adatte per percorsi ibridi che comprendono asfalto e sterrati ben battuti (come quelli delle ciclabili).
Ci risentiamo presto
Stefano Tuveri
PROSEGUE CON LA TERZA PUNTATA: LA SCELTA DELLA LARGHEZZA DEGLI PNEUMATICI PER BDC


Gomma Panaracer 35 mm Gravel , con la tua formula 5.9 Bar ant.
7.6 Bar post.
max pressione ammessa da produttore per tubeless 4.4 Bar .
Che tipo di correzione bisogna introdurre nella formula ?
"Mi piace""Mi piace"
Le corrette pressioni per pneumatici tassellati si determinano in modo differente rispetto alla formula (semplice, e per questo motivo ve l’ho messa a disposizione) per coperture liscie.
Ciascuno pneumatico tassellato invece richiede di essere studiato singolarmente; i valori corretti di pressione dipendono da parametri che non sono presenti nelle gomme liscie (a cominciare dai tasselli, per i quali sono fondamentali la spaziatura, l’altezza, la superficie). E’ un’operazione piuttosto complessa, per la quale non esiste una singola formula ma uno studio che richiede più formule e calcoli in successione.
Questo lavoro viene effettuato all’interno dell’analisi personalizzata del biker, come questa: https://bikeplani.wordpress.com/2019/06/28/nel-nostro-laboratorio-ingegnerizzazione-personalizzata-della-vostra-mountain-bike/
Il biker indica i copertoni che utilizza, e gli vengono fornite tutte le informazioni (pressioni ottimali a seconda del tipo di forndo stradale, relativo coefficiente di attrito volvente che determina una delle forze che si oppongono al moto).
L’analisi personalizzata può venir richiesta da chiunque sia interessato. Eventualmente si può richiedere anche solo la parte che riguarda lo studio degli pneumatici.
Invece, per coloro che si fanno allestire da noi la mountain bike, l’analisi personalizzata viene fornita assieme alla mtb (anche perchè viene utilizzata per ottimizzarla, scegliendo i rapporti della trasmissione, il tipo di copertoni, e in generale tutto ciò che consente di “cucire addosso” la mtb sul biker, rendendola la bici perfetta per lui).
Per quanto riguarda i valori di pressione massima indicati dai produttori, basti pensare che il parametro fondamentale per determinare la pressione “giusta” è il peso di bici+ciclista. Penso basti questo per capire quale validità (praticamente nulla) possano avere i valori di pressione indicati in modo così generico dai produttori (possono essere considerati come dei valori di sicurezza, oltre i quali il produttore non garantisce la tenuta della gomma, ma non certo dei valori che minimizzino l’attrito volvente)
Stefano Tuveri
"Mi piace""Mi piace"
Ciao Stefano, articolo molto interessante, complimenti per il lavoro e le capacità divulgative.
Leggevo quello che dichiara Schwalbe sul loro sito a proposito degli pneumatici larghi. Se non ho capito male la loro teoria è che su pneumatici sopra una certa sezione (da 35 mm di larghezza in su con pressioni medie di 3/4 bar) la componente principale della resistenza al rotolamento è data dall’energia assorbita per il ciclo di isteresi della deformazione della gomma del fianco del pneumatico. Quindi, a pari pressione, pneumatici più larghi e dal fianco più flessibile (come i Big Apple da 60mm) scorrono meglio di pneumatici più stretti ma con fianchi più rigidi (come i Marathon 37 mm).
Penso che uno pneumatico corsa (23/25mm) a 8 bar sia fuori dal confronto e nessuno metta in dubbio che scorra molto meglio di entrambi gli pneumatici sopra, date anche le limitatissime deformazioni del fianco.
Quindi l’affermazione generale che pneumatici larghi scorrono meglio degli stretti, se contestualizzata bene su determinate larghezze e tipologie di pneumatici turistici può avere un certo senso. A pari scorrevolezza, sacrificando la robustezza dei marathon puoi avere un pneumatico più confortevole gonfiato a pressioni minori. Uno scambio sensato per un uso cittadino, non certo per un viaggio off-road di centinaia di km.
"Mi piace""Mi piace"
Ciao Daniele, mi fa piacere che apprezzi queste pubblicazioni, e ti ringrazio per l’attenzione che presti loro.
In questi giorni sono impegnatissimo nell’attività di laboratorio, e son già stato “sollecitato” da altri frequentatori abituali del sito (ma quanti siete diventati? Il numero delle visite è più che decuplicato negli ultimi mesi!) a pubblicare qualche nuova analisi tecnica (insomma, a pulire le mani da olio e grasso, e rimetter mano alla teoria).
Prometto che a breve, appena completati gli allestimenti di mtb che ci son stati richiesti prima di Pasqua, tornerò alla mie amate Fisica e Meccanica (ho già alcuni articoli quasi pronti, spero che l’attesa venga ripagata dall’interesse che dovrebbero suscitare).
Ma veniamo alle “teorie Schwalbe”. Appena potrò, andrò a leggermi cosa dicono questa volta. Quando lessi le spiegazioni che diedero sul loro sito un paio d’anni fa (ovvero quando scrissi quest’articolo; perché poi confesso di non aver più provato interesse a “informarmi” presso di loro), ricordo che trovai quantomeno bizzarre le loro spiegazioni. L’attrito volvente infatti è un fenomeno piuttosto complesso, in cui entrano in gioco tanti fattori, e ciascuno di questi fattori va a sua volta analizzato in tutti i suoi aspetti.
Invece loro banalizzano, enfatizzando un unico aspetto (quello che conviene loro, in quanto favorevole ai loro prodotti), e “dimenticando” tutto il resto.
Quella volta, si limitavano ad affermare genericamente che “pneumatici più larghi hanno, a parità di pressione, minore attrito volvente, perché l’impronta è più corta e larga”. Su quelle loro affermazioni, scrissi la “risposta” presente nell’articolo.
Come ti dicevo, non ho letto le loro “ultime”. Però, già su quanto hai riportato, si possono fare delle considerazioni importanti:
– è vero che l’isteresi della gomma è la causa principale della perdita di energia, che macroscopicamente noi “vediamo” e definiamo come “resistenza al rotolamento”, ma questo vale anche per pneumatici da 18mm, e non certo soltanto per i loro cicciogommoni da 60mm.
– ricordiamo cos’è l’isteresi, anche per i non addetti ai lavori: è quella parte di energia che un corpo assorbe durante la deformazione senza più restituirla quando torna alla forma originaria. Questa energia, lo si capisce anche intuitivamente, dipende anche dalla massa dell’oggetto che viene deformato, e qui è davvero arduo sostenere che un cicciogommone da 60mm abbia, rispetto a una gomma da 35mm, un bilancio di isteresi più positivo in termini assoluti (potrebbe forse averlo in termini relativi, se ad esempio dovesse andar persa per isteresi nel ciccio60 il 30% della deformazione – cifra sparata a caso giusto per ragionarci su – e nel 35mm invece il 40%; ma se ciccio ha massa doppia del 35mm, hai voglia ad avere un 10% di isteresi relativa in meno, quando devi deformare una massa pari al 200% di quella del 35mm… Verrebbe il sospetto che, in termini assoluti, l’isteresi penalizzi ben di più il cicciogommone; sospetto che poi è ampiamente confermato quando si va a calcolare con metodo scientifico il coefficiente d’attrito volvente)
– ultima nota: Schwalbe come al solito dimentica di guardare TUTTO il fenomeno fisico di cui parla. In uno pneumatico stretto, a parità di pressione, l’impronta è più stretta (e più allungata) che in uno pneumatico largo, e quindi comporta una MINORE deformazione del fianco (in parole povere, si dovrà “spanciare” di meno durante il rotolamento). Pertanto, messa in questi termini (ovvero, paradossalmente, seguendo il loro discorso), la situazione si mostra sfavorevole al ciccio rispetto al 35mm.
Ma, come detto, è comunque una rappresentazione parziale e “giocattolesca” di un fenomeno fisico ben più complesso, e che merita ben altra trattazione.
Facciamo così: appena mi libero un po’ di tempo, prendo in considerazione i due penumatici (ciccio e smilzo), calcolo esattamente il coefficiente di attrito volvente per differenti situazioni (perché, ovviamente, la pressione “giusta” per una gomma sarà diversa a seconda che si pedali su asfalto buono, su asfalto scassato, su sterrato, e così via), e poi pubblico un nuovo “diamo i numeri” dedicato proprio a questo argomento, visto che interessa tanti di voi
Ci sentiamo presto
Stefano Tuveri
"Mi piace""Mi piace"
Grazie della risposta, davvero è un argomento interessante, su internet si sprecano le discussioni da bar, ma test indipendenti sono rari. Ancora più modelli che possano risolvere il problema in maniera accurata. Il fenomeno credo sia davvero molto complesso, implicando talmente tanti fattori che anche un modello matematico forse rischia di partire da semplificazioni e assunzioni troppo spinte. Il solo fenomeno dell’isteresi dipende da talmente tanti fattori che davvero penso sia di difficile modellizzazione, i materiali non sono gli stessi per tutti gli pneumaitci, il tipo di mescole, l’intreccio e il tipo delle fibre, la stratificazione di più strati di materiale diverso compresi rinforzi interni dei più svariati materiali come il kevlar. C’è una correlazione proporzionale alla massa ma poi intervengono davvero troppi altri fattori. A pari peso ci sono pneumatici con fianchi molto flessibili e sottili ma con un battistrada consistente provvisto di rinforzi, altri con fianchi molto spessi e rinforzati e battistrada più sottile. Chiaramente avranno isteresi ben diverse nonostante abbiano la stessa massa. Io possiedo una bici che monta BigApple da 700×50 e posso confermare che la spalla è veramente sottile e deformabile. Molto più di altri pneumatici di pari larghezza. Ma non pesano molto meno di altri pneumatici simili a causa di un rinforzo centrale in kevlar. Molta meno isteresi ma stesso peso quindi.
È interessante vedere che sono stati fatti test da laboratori indipendenti su rulli, che confermano che lo stesso pneumatico in diverse larghezze ha un resistenza minore per diametri maggiori. Bykerollingresistance ha testato i Marathon nelle larghezze di 32, 35, 37 e 42 rilevando che il pneumatico che offriva più resistenza era il 32. Non tanto per la larghezza ma per una costruzione piu rigida della carcassa. Apparentemente diversa dagli altri 3 modelli che erano sugli stessi valori di resistenza. C’è un pneumatico slick schwalbe, il Big One, da 60mm, che pesa solo 400 grammi, e performa a basse pressioni come i top di gamma da corsa, nonostante pesi il doppio abbondante…
L’argomento è davvero degno di considerazione, penso interessi molti, tanti falsi miti, ma pochi test in laboratorio lasciano aperti tanti dubbi sicuramente. Qualsiasi contributo è davvero benvenuto. Aspetto di leggere qualche approfondimento su queste pagine appena possibile. Ti ringrazio per l’impegno profuso a favore di tutti gli interessati. Ho letto nei tuoi articoli tante mozioni che condivido e che spesso sono poco evidenti ai più.
"Mi piace""Mi piace"
Torno volentieri sull’argomento, con una breve ma fondamentale premessa:
Questi articoli son scritti per consentire anche ai non addetti ai lavori (intendendo come tali anche quelli che hanno poche o nulle nozioni di fisica di base) di comprendere meglio cosa c’è “dietro” la loro bicicletta. Va da se che rendere comprensibili a tutti argomenti estremamente complessi, è un lavoro difficile che implica di riportare ciascun argomento ai concetti che vi stanno alla base, senza avventurarsi in dettagliate spiegazioni teoriche, e meno che mai nell’esposizione di formule, che sarebbero arabo anche per chi abbia una cultura scientifica universitaria ma non abbia studiato specificamente questi argomenti.
Intendo dire che, per padroneggiare questi argomenti, è necessario un percorso di studi in ingegneria meccanica, seguito da anni di studio su questi temi specifici. Va da se quindi che, davanti alle conclusioni che riporto in queste analisi, avete una sola possibilità: fidarvi.
Fidarvi non tanto del sottoscritto, quanto della professionalità che è specifica di una ben determinata professione, che prevede la conoscenza approfondita di questi argomenti. Io so bene che oggi google ci dà l’impressione di poter accedere a qualunque informazione e farla nostra. Purtroppo non è così, quando si tratta di temi particolarmente complessi si possono fare solo due cose: studiarli per anni, oppure affidarsi a chi quello studio l’ha effettivamente svolto.
Bene, detto questo, vediamo di rispondere ad alcuni argomenti citati da Daniele:
-Bikerollingresistence: questo sito, o meglio la persona che ci sta dietro, purtroppo effettua le sue prove partendo da condizioni totalmente (e grossolanamente) sbagliate. Infatti, la resistenza al rotolamento su una superficie curva (come quella su cui fa rotolare gli pneumatici) è malamente alterata rispetto alla resistenza che si ha su un piano (come quello su cui invece gli pneumatici rotolano nella realtà). E’ alterata perché cambia radicalmente la forma dell’impronta, allargandola e accorciandola, e soprattutto avvantaggiando in questo modo le gomme più larghe rispetto a quelle di larghezza minore. Questo fatto è basilare quando si vuole testare uno pneumatico, e ignorarne l’importanza toglie qualunque credibilità ai risultati ottenuti (e soprattutto alla competenza di chi effettua le prove).
-Ancora, il piano di rotolamento non è liscio, ma presenta quelle tacche che, ancora, alterano totalmente gli esiti delle prove. Infatti, quelle tacche ad altro non corrispondono che a delle irregolarità del terreno. Quindi, i risultati ottenuti non hanno niente a che vedere con la resistenza al rotolamento su un fondo regolare come quello asfaltato (per il quale sono previste molte delle gomme testate). Ma, ancor peggio, in presenza di irregolarità ogni gomma ha la sua pressione “giusta”, per cui testarle con pressioni prese a caso non ha alcun senso (ma su questo ci torniamo nel punto seguente)
-Veniamo poi a quello che è il punto più importante: ciascuno pneumatico ha la sua pressione “giusta” per ciascun tipo di terreno, il che significa che, per ciascun tipo di fondo stradale, esiste un valore di pressione (specifico per quello pneumatico) che ne minimizza la resistenza al rotolamento. Volendo considerare solo il fondo stradale asfaltato in perfette condizioni (così da limitare il discorso, che altrimenti sarebbe estremamente ampio), ciascuno pneumatico ha la “sua” pressione. Quindi non ha nessun senso quello che fa bikerolleccetera, che testa gli pneumatici confrontandoli alla stessa identica pressione. E’ come se, ignorando il numero di scarpa di ciascuno, si dessero a un gruppo di persone scarpe tutte dello stesso numero e poi si andasse a vedere chi cammina meglio (spiegata in questi termini, si capisce bene come si tratti di un’idiozia). Quindi, per fare una prova che abbia significato, si deve innanzitutto determinare la pressione “giusta” (ovvero che minimizzi la resistenza al rotolamento) per ciascun tipo di pneumatico, e confrontare i diversi pneumatici dopo averli portati a questa pressione (e, a parità di “composizione”, uno pneumatico più stretto ha, su asfalto, una pressione “giusta” più alta rispetto a uno largo, per cui è ovvio che se lo si testa a pressioni basse, lontanissime da quella corretta per lui, abbia prestazioni peggiori della ruota di una carriola). Eventualmente, in ulteriori prove si possono poi considerare degli scostamenti percentuali da questa pressione “giusta” (ad esempio, abbassandola del 20% in tutte le gomme, perché magari si vuole una guida più confortevole) e fare un’altra prova in queste condizioni. Capite bene che quindi, i pur volenterosi test di Bikerollpuntinipuntini non servono assolutamente a niente, se non a dare informazioni sbagliate.
-Passiamo ora a un fenomeno fisico molto importante, e fondamentale nella resistenza al rotolamento, di cui in rete si leggono cose totalmente sballate. Parliamo dell’isteresi. Su questo fenomeno si leggono cose che, in quando a livello di boiata, ricordano quegli articoli “tecnici” in cui si afferma che alleggerire le ruote di 300 grammi migliora l’accelerazione di una bici (il che è vero, ma la migliora di 600 grammi fratto gli 80kg di bici+bike, ovvero dello 0,75%, il che è ben diverso dal mirabolante incremento di prestazioni che viene millantato), o che la flessione dell’acciaio comporti perdite di energia (anche qui è vero, ma siamo sull’ordine dello 0,2-0,3%, peraltro in buona parte recuperate grazie all’elasticità del materiale, e ampiamente compensate dal maggior confort con conseguenti vantaggi anche in termini di prestazioni).
Ma torniamo all’isteresi: io capisco benissimo voi che, non essendo addetti ai lavori, ne fraintendete il significato, dato che le informazioni di cui venite bombardati distorcono completamente questo concetto. Del resto, il motivo per cui dedico del tempo a scrivere su queste pagine, è proprio quello di provare a contrastare queste sciocchezze che vi vengono rifilate. Partiamo quindi dallo spiegare che cos’è l’isteresi, e pensiamo a una molla: noi spendiamo dell’energia per comprimere una molla; quando poi la rilasciamo, la molla ci restituisce un’energia minore di quella che le avevamo fornito per comprimerla. Bene, quest’energia che è andata persa, si dice che è stata dissipata durante un ciclo di isteresi (ovvero un ciclo in cui la molla torna alla posizione di partenza).
So bene che, nelle trattazioni “scolastiche”, si considera la molla come priva di isteresi, e tale che restituisca tutta l’energia elastica che accumula quando viene compressa, ma questo avviene nel mondo ideale (che non esiste, mentre in quello reale dobbiamo rassegnarci a queste degradazioni di energia, che ahinoi pian piano si trasforma in calore).
Perché quest’introduzione? Perché non tutti i materiali hanno le stesse perdite di energia. Un copertone perde ben più energia di una molla, deformandosi e tornando alla forma iniziale. Ma soprattutto, il fatto che un materiale opponga meno resistenza alla deformazione, non significa affatto che abbia una minore isteresi e quindi disperda meno energia, tutt’altro! Pertanto, il fatto che uno pneumatico abbia fianchi che si piegano offrendo poca resistenza non c’entra nulla col fatto che disperda meno energia. Una molla d’acciaio offre una grande resistenza alla deformazione, ma disperde ben meno energia di una molla di marzapane. Quello che conta non è quanta resistenza opponga alla deformazione, ma quanta dell’energia assorbita per deformarsi poi restituisca riprendendo la forma originaria.
Come ho detto all’inizio, queste materie sono molto complesse. Ma se è vero che non sono alla portata di chi non ha una formazione specifica, è altrettanto vero che, chi quella formazione ce l’ha, è invece in grado di padroneggiare l’argomento e di arrivare a risultati che sono oggettivamente corretti. Non troverete mai in rete un modello matematico che vi consenta di calcolare da voi la resistenza al rotolamento di uno pneumatico, per il semplice fatto che non si tratta di una semplice formuletta, ovvero un’equazione in cui, inserendo un paio di valori, si arriva al risultato. Il modello matematico è estremamente più complesso, consta di un sistema di equazioni, a loro volta parametriche, e metterlo davanti a un profano è come mettere davanti a un pilota di lambretta il quadro comandi di un Boeing.
E quindi? E quindi posso solo dirvi che le grandezze che concorrono a determinare la resistenza al rotolamento di uno pneumatico, influenzano il risultato con modalità e “peso specifico” molto diversi da quelli che si è portati (o che si viene portati) a pensare.
E infine: certo che si può determinare con precisione la resistenza al rotolamento, inserendo nel modello matematico tutte le grandezze che la determinano, compresa la tipologia dei materiali che compongono gli pneumatici che, e so che potrà apparirvi strano, hanno un’influenza molto minore di quanto si creda (siamo in una situazione analoga a quella dove si vuol far credere che 200g risparmiati sulle ruote determinino prodigiosi vantaggi, ma questo è vero nel magico mondo del marketing, non in quello reale). E poiché in Fisica tutto deve essere poi validato sperimentalmente, è possibile verificare la corrispondenza con quanto calcolato teoricamente, ed è possibile anche in un piccolo laboratorio che non disponga di grossi mezzi (ed è infatti quello che faccio), a patto che vi sia dietro la necessaria professionalità (e che si lascino perdere metodi come quelli alla bicyclerollingblablablà)
Spero di esservi stato di aiuto, non mi resta che suggerirvi di fidarvi della professionalità, che è una cosa seria, perché certi argomenti, anche con tutta la buona volontà, non li si può comprendere se non si ha una formazione specifica di alto livello
Stefano Tuveri
"Mi piace""Mi piace"
Intanto ti ringrazio del tempo che dedichi e delle tue risposte approfondite che leggo sempre con molta attenzione, mi risulta tutto molto chiaro. Concordo in effetti che il test su rullo di metallo corrugato così piccolo non sia completamente rappresentativo delle condizioni in strada per i motivi citati. Le case produttrici hanno apparecchiature molto più costose e professionali, come rulli ricoperti di asfalto con diametri molto più grandi, i risultati però potrebbero essere strumentalizzati a fini di marketing come ben dici o comunque semplicemente non divulgati.
Ma credo anche che modellizzare correttamente le perdite di energia per materiali con deformazioni e geometrie così complesse senza conoscere l’esatta composizione fisica non sia compito facile, sicuramente il margine di errore c’è anche su un modello matematico. Quindi leggo con interesse sia dei risultati teorici che di quelli sperimentali, senza a prescindere scartare nessun risultato, ne mettere in dubbio il lavoro di nessuno. C’è anche ad esempio chi ha provato a strumentare una bici e replicare un test su strada, ma temo che le variabili in gioco siano talmente elevate da rendere il test inaffidabile.
Alcuni produttori vedo che si schierano spesso sulla linea Schwalbe, sbandierano sui loro siti grafici e test che dimostrano la minor resistenza di pneumatici più larghi. (Continental, Rene Herse…). Laboratori indipendenti come Wheels Energy confermano in parte questi risultati.
Personalmente sono scettico, anche solo per esperienza diretta sulla stessa strada in piano appena asfaltata con gli pneumatici da 25 mi pare di fare molta meno fatica che coi Big Apple 50 mm a pari pressione, e velocità costante. Trovo però davvero incredibile che ci sia tanta confusione a riguardo.
Leggerò con interesse qualsiasi aggiornamento a riguardo o approfondimento tu voglia fare, per il momento grazie del tuo lavoro.
"Mi piace""Mi piace"
Sono io che ringrazio te, Daniele, e tutti coloro che dedicano del tempo a leggere questi miei articoli.
Come ti dicevo, quelle prove sul rullo distorcono pesantemente quella che è la reale resistenza al rotolamento, per i motivi che vi ho spiegato. La distorcono a tal punto da ribaltare la realtà, e ignorano talmente grossolanamente i principi base dell’attrito volvente, da mostrare che lo stesso autore è palesemente non competente in materia.
Capisco anche le tue perplessità sulle differenze tra materiali e composizioni negli pneumatici, che ti fanno supporre significative differenze di isteresi (e conseguentemente di resistenza al rotolamento). Prometto di fornirvi qualche esperimento pratico che vi faccia toccare con mano quale sia la loro influenza, ma per il momento accontentatevi di questa osservazione, ovvero: l’isteresi in uno pneumatico è elevatissima, perchè non è una molla (che resistuisce buona parte dell’energia assorbita), ma è costituito da un materiale con bassissima elasticità, che all’interno del sistema pneumatico+aria ha un comportamento quasi passivo. Ovvero, così è ancora più chiaro: a restituire una parte dell’energia assorbita, è in netta prevalenza l’aria. Gomma, kevlar, e tutto ciò che può comporre uno pneumatico, costituiscono una mescola con un’elasticità sufficiente giusto a fargli assumere nuovamente la posizione inziale, senza che sia in grado di restituire la forza ricevuta, come invece fa una molla in acciaio.
Ecco quindi che, se pure una nuova mescola dovesse avere una migliore elasticità rispetto alle altre, stiamo parlando comunque di un vantaggio che percentualmente ha un peso irrisorio (giusto per capirci ragionando sui numeri: che una mescola abbia un’elasticità maggiore del 10%, diventa comunque del tutto insignificante se questo porta il valore dell’energia persa dal 95% al 94,5%).
Messa la questione in questi termini, si capisce come le nuove mescole possano essere importanti per ottenere coperture che garantiscano la necessaria resistenza pur essendo più leggere (vantaggio enorme, quindi non stiamo parlando di progressi tecnologici farlocchi, ma reali), ma ai fini della resistenza al rotolamento i benefici sono, come detto, di entità ben inferiore a quella che si è portati a credere (ma forse è più giusto dire “si è indotti”).
p.s.: che dei copertoni da 50mm abbiano resistenza al rotolamento superiore a quelli da 25mm, mi sento di potervelo garantire anche senza bisogno di ricorrere al modello matematico (a volte si ha l’impressione che certi produttori vivano in un perenne primo di aprile…)
"Mi piace""Mi piace"